A few weeks ago, we saw how nature’s preference of perceiving things in log-scale and of growing things in gnomons leads to occurrences of Fibonacci numbers in the data-sets. This week, we will discover another fundamental reason why Fibonacci numbers may emerge in a dataset.

All of us know the formula of combinations, where one has to choose “k” things from a set of “n” things. The possible ways in which this choice can be made is given by a formula:

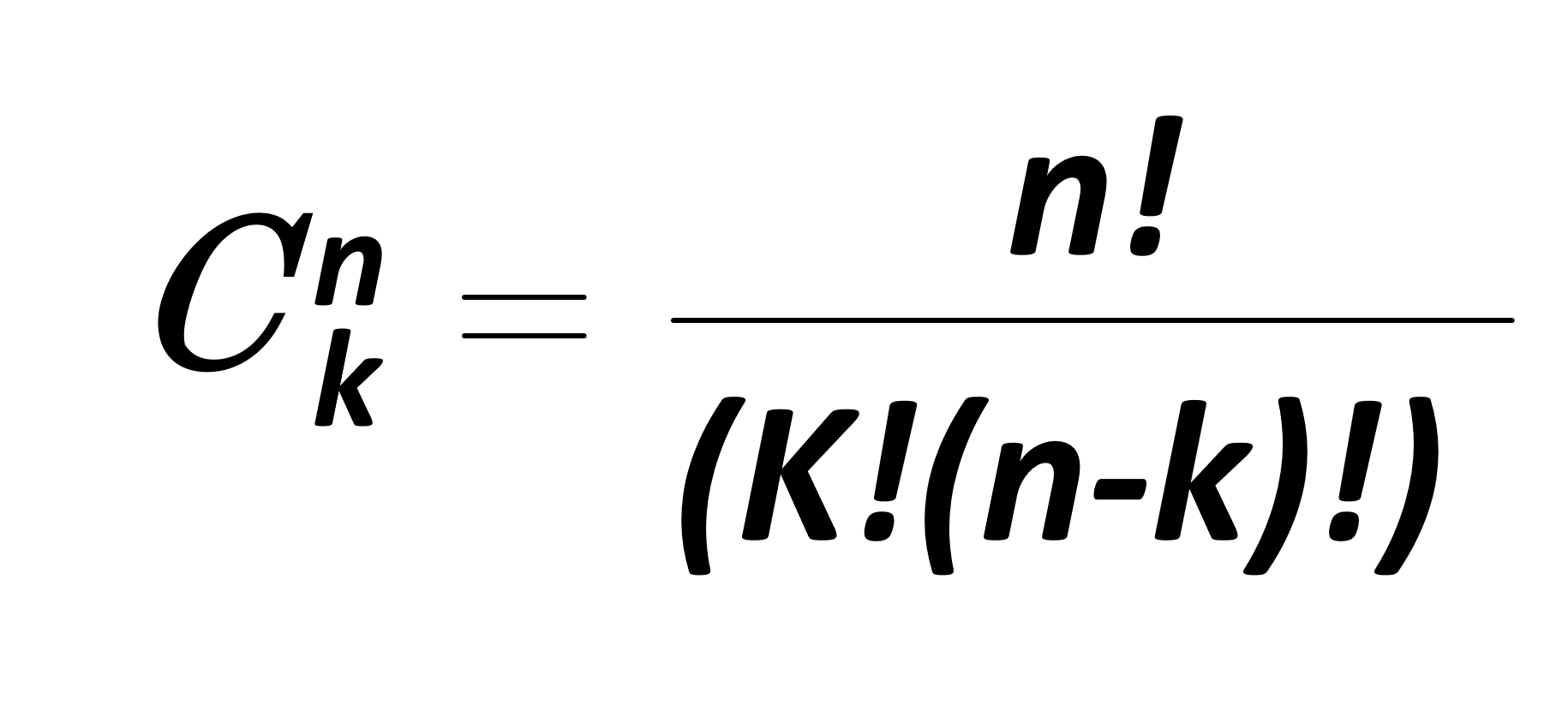
While nearly all of us may be aware of this result, many of us may not be aware of a link between combinations and Fibonacci Numbers. Have a look at the table below, which depicts the number of combinations for various n and k: